Control Your Universe

As the guy snatches your hand-bag, you started going after him. Moments later, figuring that out-running this guy is simply beyond your wildest imagination, you slow down to a stop and continue to yell at him "Don't let me catch you, you son of a...". Okay stop right there, we've just seen physics in action:

1. Your speed increases.
2. Your speed reaches its max.
3. Your speed reduces.
4. Come to a stop.

Overly simplified, but you get the idea. Nothing jumps from stationary to a high speed, nothing comes to a standstill immediately. Speed changes gradually. So just in case you're wondering, things you saw in Click weren't real:

The Crazy Chase
Say, it all started when you were walking, with an initial velocity denoted by u. Let’s start evaluating the whole crazy chase from the moment he snatched your hand bag. In the accelerating phase (first half), you started running like a mad dog and then reached your peak velocity, vc. That’s when you decided to give it up and go into a decelerating phase (second half), slowing down from your top speed vc, to a stop.


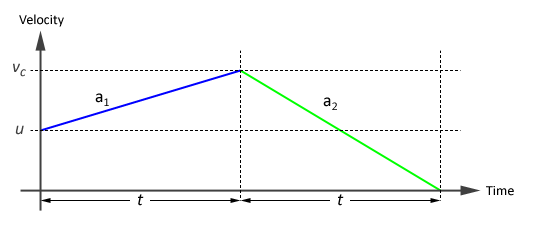
Let’s make an assumption that the accelerating phase (first half) takes as much time as the decelerating phase (second half). Time required for each phase is denoted by t. So for the accelerating phase, we get:

And for the decelerating phase, we get:As you stopped at the end of decelerating phase, v is zero, that gives us:

Equation (1) equals to equation (2):Now consider the distance you’ve travelled, here’s how it would look like in a graph. S represents the total distance, from the moment you started chasing him, to the moment you stopped. Though both accelerating and decelerating phases take the same amount of time, the distances travelled are different due to difference in velocity.
Denoting the distance travelled in the accelerating phase with x, we get:
As the total distance travelled is S, it is clear that you travelled S-x in the decelerating phase:
Substituting Equation (2) gives:
Substituting Equation (3) gives:
Substituting Equation (4) into (5) gives:

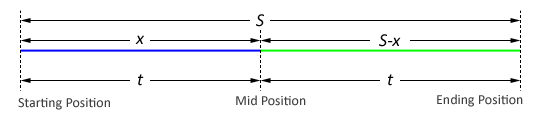
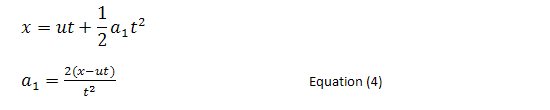
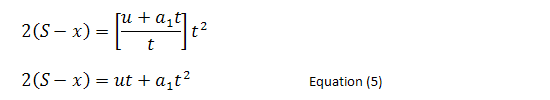
So… what’s the use of analyzing this crazy chase you ask?

To derive equations that make subtle movements in game feel smoother and more natural. Take for an example selection highlight that moves from one menu item to the other. The selection highlight does not have to jump among menu items because that looks kind of stiff; with its movements interpolated, the selection highlight should smoothly glide between two menu items.

Of course these formulas are not limited to just movements, they can be used to morph any variable from one value to another (e.g. colors, rotation angle).